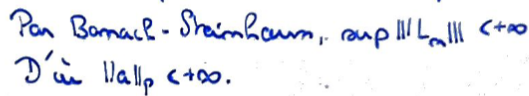Démonstration du théorème de Banach-Steinhauss :

On pose \(E_k\) l'ensemble des points où toutes les normes d'applications linéaires sont bornées par \(k\).

On peut voir que les \(E_k\) sont fermés par caractérisation séquentielle, et que leur union est \(E\).

D'après le Théorème de Baire, l'un des \(E_k\) est d'intérieur non vide \(\to\) on peut prendre une boule à l'intérieur, qu'on peut prendre fermée.

Par symétrie et convexité, on peut centrer cette boule en \(0\).

On obtient donc que les \(L\) sont uniformément bornés.

On suppose que $$\lVert x\rVert\leqslant r\implies \lVert Lx\rVert\leqslant k.$$
Montrer que pour tout \(x\in E\), \(\lVert Lx\rVert\leqslant\frac kr\lVert x\rVert\).

Changer l'échelle de \(x\) pour que sa norme soit inférieure à \(r\).
Soit \(x\in E\). On a $$\left|\!\left|\frac r{\lVert x\rVert}x\right|\!\right|\leqslant r.$$

Appliquer la donnée de l'énoncé.
On a alors $$\left|\!\left|\frac r{\lVert x\rVert}Lx\right|\!\right|\leqslant k.$$

Passer les coefficients de l'autre côté par homogénéité.

Ce qui nous donne par homogénéité $$\lVert Lx\rVert\leqslant\frac kr\lVert x\rVert.$$

Démontrer la proposition suivante :

Linéarité ok par continuité de la somme et de la multiplication par un scalaire.

La suite est bornée pour tout \(x\).

On applique Banach-Steinhauss, ce qui nous donne le fait que la limite est continue (par caractérisation avec la linéarité et la norme induite).

Soit \(p\in[1,+\infty]\) et \(q\) l'exposant conjugué tq \(\frac1p+\frac1q=1\).
Soit \((a_n)_{n\in\Bbb N}\) une suite de \({\Bbb C}^n\) tq $$\forall (b_n)_{n\in\Bbb N}\in l^q,\quad\sum_{n\in{\Bbb N}}a_nb_n\text{ converge}.$$
Montrer que \((a_n)_{n\in\Bbb N}\in l^p\).

On pose pour \(n\) donné la fonction \(L_n\) qui associe à la suite \(b\) la somme partielle d'ordre \(n\) (c'est bien une forme linéaire).

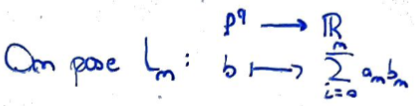
D'après l'Inégalité de Hölder, \(L_n\) est continue par majoration de la norme (on peut l'appliquer sans soucis puisque les sommes sont partielles).

Puisqu'on est dans le cas d'égalité dans l'Inégalité de Hölder, on a en fait exactement la norme.

\(L_n\) est simplement bornée par hypothèse de l'énoncé (convergence de la série).

Le Théorème de Banach-Steinhauss nous donne le fait que les \(L_n\) sont en fait uniformément bornés, ce qui donne que \(\lVert a\rVert_p\lt +\infty\), et donc que \(a\in l^p\).